10\frac1001 is undefined .
Why some people say it’s true: Dividing by 0 00 is not allowed .
Why some people say it’s false: 10=∞.\frac10 = \infty.01=∞.
Can you see which of these is the adjust explanation ?
The statement is true \color { # 3D99F6 } { \textbf { on-key } } true .
Proof:
If 10=r \frac10 = r01=r were a real number, then r⋅0=1, r\cdot 0 = 1, r⋅0=1, but this is impossible for any r. r.r. See division by zero for more details. □_\square□
There are some coarse responses to this logic, but they all have versatile flaws .
Rebuttal: In calculus,
10\frac10
0
1
equals
∞. \infty.
∞
.
Reply : This instruction is faulty for two reasons. First, eternity is not a substantial number. The proof demonstrates that the quotient 10\frac1001 is undefined over the real numbers .
It is on-key that, in some situations, the indeterminate form 10\frac1001 can be interpreted as ∞ : \infty : ∞ : for exemplify, when taking limits of a quotient of functions. But flush this is not always true, as the comply example shows :
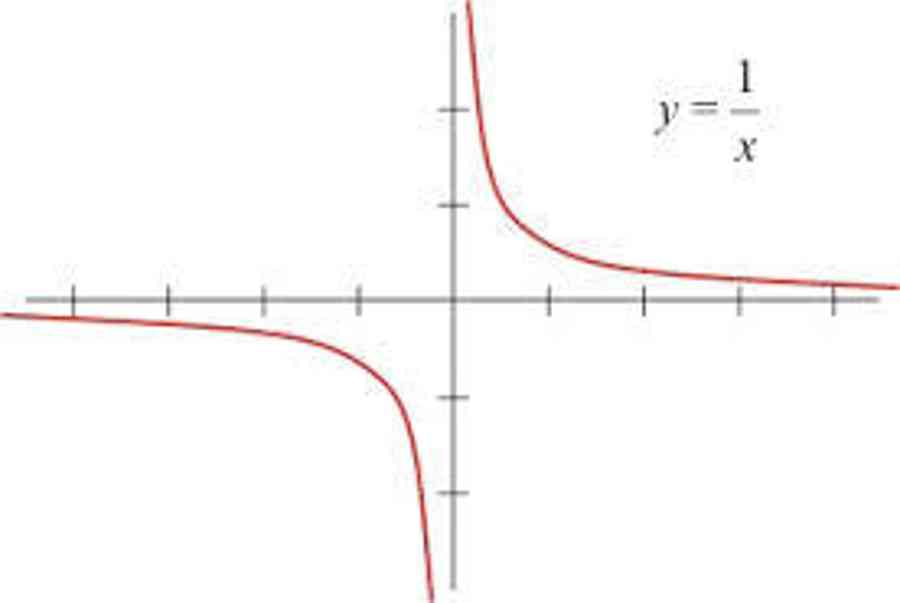
Consider limx→01x. \lim\limits_ { x\to 0 } \frac { 1 } { ten } .x→0limx1 .
Approaching from the justly, limx→0+1x=+∞. \lim\limits_ { adam \to 0^+ } \frac { 1 } { x } = + \infty. x→0+limx1=+∞.
Approaching from the left field, limx→0−1x=−∞. \lim\limits_ { x \to 0^- } \frac { 1 } { ten } = – \infty. x→0−limx1=−∞ .
In order for 10 \frac { 1 } { 0 } 01 to be coherent, the limits from both directions should be equal, which is distinctly not the subject here .Rebuttal : What about on the Riemann celestial sphere ?
Reply : For certain building complex functions, it is commodious and coherent to extend their domain and compass to C∪ { ∞ }. { \mathbb C } \cup \ { \infty\ } .C∪ { ∞ }. This set has the geometric social organization of a sphere, called the Riemann sphere. For case, suppose a, boron, vitamin c, district attorney, b, hundred, district attorney, b-complex vitamin, hundred, d are complex numbers such that ad−bc≠0. ad-bc\ne 0.ad−bc=0. then the affair farad ( omega ) =az+bcz+d fluorine ( omega ) = \frac { az+b } { cz+d } f ( omega ) =cz+daz+b can be extended by defining farad ( −dc ) =∞ f\left ( -\frac dc\right ) = \infty fluorine ( −cd ) =∞ and fluorine ( ∞ ) =ac farad ( \infty ) = \frac ac f ( ∞ ) =ca ( \big ( ( or f ( ∞ ) =∞ fluorine ( \infty ) = \infty farad ( ∞ ) =∞ when c=0 ) .c=0\big ) .c=0 ). This makes fff a bijection on the Riemann sphere, with many nice properties .
thus there are situations where 10\frac1001 is defined, but they are defined in a tightly controlled way. It is hush the case that 10\frac1001 can never be a real ( or complex ) number, so—strictly speaking—it is undefined .
See the consequences of assuming that 10\frac { 1 } { 0 } 01 is defined for yourself in the watch problem :
Incorrect factoring
Multiplying unknown variables
False substitution
Introducing
−b2-b^2
−
b
2
Dividing by zero
What is ill-timed with the following “ proof ” ?
Let a=b=1a = b=1a=b=1, then a+b=b.a+b=b.a+b=b .
- Step 1:
a2=aba^2 = ab
a
2
=
a
b
- Step 2:
a2−b2=ab−b2a^2 – b^2 = ab – b^2
a
2
−
b
2
Read more: Ex on the Beach (British series 6)
=
a
b
−
b
2
- Step 3:
(a+b)(a−b)=b(a−b)(a+b)(a-b) = b(a-b)
(
a
+
b
)
(
a
−
b
)
=
b
(
a
−
b
)
- Step 4:
a+b=b(a−b)a−ba+b= \dfrac{b(a-b)}{a-b}
a
+
b
=
a
−
b
b
(
a
−
b
)
- Step 5:
a+b=ba+b = b
a
+
b
=
Read more: Clint Barton (Marvel Cinematic Universe)
b
decision : By substituting in a=b=1, a = b = 1, a=b=1, we have 1+1=1 ⟹ 2=1.1+1 = 1 \implies 2 = 1.1+1=1⟹2=1 .
See Also